116. 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
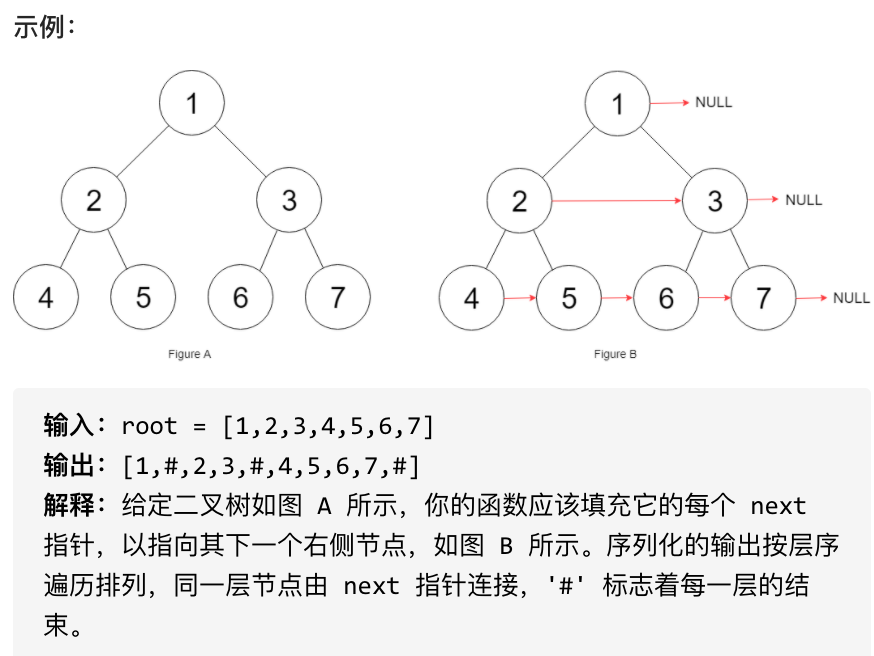
}填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
思路
注意题目提示内容,:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
基本上就是要求使用递归了,迭代的方式一定会用到栈或者队列。
递归
一想用递归怎么做呢,虽然层序遍历是最直观的,但是递归的方式确实不好想。
如图,假如当前操作的节点是 cur:
最关键的点是可以通过上一层递归 搭出来的线,进行本次搭线。
图中 cur 节点为元素 4,那么搭线的逻辑代码:(注意注释中操作 1 和操作 2 和图中的对应关系)
if (cur->left) cur->left->next = cur->right; // 操作1
if (cur->right) {
if (cur->next) cur->right->next = cur->next->left; // 操作2
else cur->right->next = NULL;
}理解到这里,使用前序遍历,那么不难写出如下代码:
class Solution {
private:
void traversal(Node* cur) {
if (cur == NULL) return;
// 中
if (cur->left) cur->left->next = cur->right; // 操作1
if (cur->right) {
if (cur->next) cur->right->next = cur->next->left; // 操作2
else cur->right->next = NULL;
}
traversal(cur->left); // 左
traversal(cur->right); // 右
}
public:
Node* connect(Node* root) {
traversal(root);
return root;
}
};迭代(层序遍历)
本题使用层序遍历是最为直观的,如果对层序遍历不了解,看这篇:二叉树:层序遍历登场! (opens in a new tab)。
遍历每一行的时候,如果不是最后一个 Node,则指向下一个 Node;如果是最后一个 Node,则指向 nullptr。
代码如下:
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != nullptr) que.push(root);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; ++i) {
Node* node = que.front();
que.pop();
if (i != size - 1) {
node->next = que.front(); //如果不是最后一个Node 则指向下一个Node
} else node->next = nullptr; //如果是最后一个Node 则指向nullptr
if (node->left != nullptr) que.push(node->left);
if (node->right != nullptr) que.push(node->right);
}
}
return root;
}
};其他语言版本
Java
// 递归法
class Solution {
public void traversal(Node cur) {
if (cur == null) return;
if (cur.left != null) cur.left.next = cur.right; // 操作1
if (cur.right != null) {
if(cur.next != null) cur.right.next = cur.next.left; //操作2
else cur.right.next = null;
}
traversal(cur.left); // 左
traversal(cur.right); //右
}
public Node connect(Node root) {
traversal(root);
return root;
}
}// 迭代法
class Solution {
public Node connect(Node root) {
if (root == null) return root;
Queue<Node> que = new LinkedList<Node>();
que.offer(root);
Node nodePre = null;
Node node = null;
while (!que.isEmpty()) {
int size = que.size();
for (int i=0; i<size; i++) { // 开始每一层的遍历
if (i == 0) {
nodePre = que.peek(); // 记录一层的头结点
que.poll();
node = nodePre;
} else {
node = que.peek();
que.poll();
nodePre.next = node; // 本层前一个节点next指向本节点
nodePre = nodePre.next;
}
if (node.left != null) que.offer(node.left);
if (node.right != null) que.offer(node.right);
}
nodePre.next = null; // 本层最后一个节点指向null
}
return root;
}
}Python
# 递归法
class Solution:
def connect(self, root: 'Node') -> 'Node':
def traversal(cur: 'Node') -> 'Node':
if not cur: return []
if cur.left: cur.left.next = cur.right # 操作1
if cur.right:
if cur.next:
cur.right.next = cur.next.left # 操作2
else:
cur.right.next = None
traversal(cur.left) # 左
traversal(cur.right) # 右
traversal(root)
return root# 迭代法
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root: return
res = []
queue = [root]
while queue:
size = len(queue)
for i in range(size): # 开始每一层的遍历
if i==0:
nodePre = queue.pop(0) # 记录一层的头结点
node = nodePre
else:
node = queue.pop(0)
nodePre.next = node # 本层前一个节点next指向本节点
nodePre = nodePre.next
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
nodePre.next = None # 本层最后一个节点指向None
return rootGo
// 迭代法
func connect(root *Node) *Node {
if root == nil {
return root
}
stack := make([]*Node, 0)
stack = append(stack, root)
for len(stack) > 0 {
n := len(stack) // 记录当前层节点个数
for i := 0; i < n; i++ {
node := stack[0] // 依次弹出节点
stack = stack[1:]
if i == n - 1 { // 如果是这层最右的节点,next指向nil
node.Next = nil
} else {
node.Next = stack[0] // 如果不是最右的节点,next指向右边的节点
}
if node.Left != nil { // 如果存在左子节点,放入栈中
stack = append(stack, node.Left)
}
if node.Right != nil { // 如果存在右子节点,放入栈中
stack = append(stack, node.Right)
}
}
}
return root
}// 常量级额外空间,使用next
func connect(root *Node) *Node {
if root == nil {
return root
}
for cur := root; cur.Left != nil; cur = cur.Left { // 遍历每层最左边的节点
for node := cur; node != nil; node = node.Next { // 当前层从左到右遍历
node.Left.Next = node.Right // 左子节点next指向右子节点
if node.Next != nil { //如果node next有值,右子节点指向next节点的左子节点
node.Right.Next = node.Next.Left
}
}
}
return root
}JavaScript
const connect = (root) => {
if (!root) return root;
// 根节点入队
const Q = [root];
while (Q.length) {
const len = Q.length;
// 遍历这一层的所有节点
for (let i = 0; i < len; i++) {
// 队头出队
const node = Q.shift();
// 连接
if (i < len - 1) {
// 新的队头是node的右边元素
node.next = Q[0];
}
// 队头左节点有值,放入队列
node.left && Q.push(node.left);
// 队头右节点有值,放入队列
node.right && Q.push(node.right);
}
}
return root;
};TypeScript
(注:命名空间‘Node’与 typescript 中内置类型冲突,这里改成了‘NodePro’)
递归法:
class NodePro {
val: number;
left: NodePro | null;
right: NodePro | null;
next: NodePro | null;
constructor(val?: number, left?: NodePro, right?: NodePro, next?: NodePro) {
this.val = val === undefined ? 0 : val;
this.left = left === undefined ? null : left;
this.right = right === undefined ? null : right;
this.next = next === undefined ? null : next;
}
}
function connect(root: NodePro | null): NodePro | null {
if (root === null) return null;
root.next = null;
recur(root);
return root;
}
function recur(node: NodePro): void {
if (node.left === null || node.right === null) return;
node.left.next = node.right;
node.right.next = node.next && node.next.left;
recur(node.left);
recur(node.right);
}迭代法:
class NodePro {
val: number;
left: NodePro | null;
right: NodePro | null;
next: NodePro | null;
constructor(val?: number, left?: NodePro, right?: NodePro, next?: NodePro) {
this.val = val === undefined ? 0 : val;
this.left = left === undefined ? null : left;
this.right = right === undefined ? null : right;
this.next = next === undefined ? null : next;
}
}
function connect(root: NodePro | null): NodePro | null {
if (root === null) return null;
const queue: NodePro[] = [];
queue.push(root);
while (queue.length > 0) {
for (let i = 0, length = queue.length; i < length; i++) {
const curNode: NodePro = queue.shift()!;
if (i === length - 1) {
curNode.next = null;
} else {
curNode.next = queue[0];
}
if (curNode.left !== null) queue.push(curNode.left);
if (curNode.right !== null) queue.push(curNode.right);
}
}
return root;
}