贪心算法:根据身高重建队列(续集)
在讲解贪心算法:根据身高重建队列 (opens in a new tab)中,我们提到了使用 vector(C++中的动态数组)来进行 insert 操作是费时的。
这里专门写一篇文章来详细说一说这个问题。
使用 vector 的代码如下:
// 版本一,使用vector(动态数组)
class Solution {
public:
static bool cmp(const vector<int> a, const vector<int> b) {
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort (people.begin(), people.end(), cmp);
vector<vector<int>> que;
for (int i = 0; i < people.size(); i++) {
int position = people[i][1];
que.insert(que.begin() + position, people[i]);
}
return que;
}
};
耗时如下:

其直观上来看数组的 insert 操作是 O(n)的,整体代码的时间复杂度是 O(n^2)。
这么一分析好像和版本二链表实现的时间复杂度是一样的啊,为什么提交之后效率会差距这么大呢?
// 版本二,使用list(链表)
class Solution {
public:
// 身高从大到小排(身高相同k小的站前面)
static bool cmp(const vector<int> a, const vector<int> b) {
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort (people.begin(), people.end(), cmp);
list<vector<int>> que; // list底层是链表实现,插入效率比vector高的多
for (int i = 0; i < people.size(); i++) {
int position = people[i][1]; // 插入到下标为position的位置
std::list<vector<int>>::iterator it = que.begin();
while (position--) { // 寻找在插入位置
it++;
}
que.insert(it, people[i]);
}
return vector<vector<int>>(que.begin(), que.end());
}
};耗时如下:

大家都知道对于普通数组,一旦定义了大小就不能改变,例如 int a[10];,这个数组 a 至多只能放 10 个元素,改不了的。
对于动态数组,就是可以不用关心初始时候的大小,可以随意往里放数据,那么耗时的原因就在于动态数组的底层实现。
动态数组为什么可以不受初始大小的限制,可以随意 push_back 数据呢?
首先 vector 的底层实现也是普通数组。
vector 的大小有两个维度一个是 size 一个是 capicity,size 就是我们平时用来遍历 vector 时候用的,例如:
for (int i = 0; i < vec.size(); i++) {
}而 capicity 是 vector 底层数组(就是普通数组)的大小,capicity 可不一定就是 size。
当 insert 数据的时候,如果已经大于 capicity,capicity 会成倍扩容,但对外暴漏的 size 其实仅仅是+1。
那么既然 vector 底层实现是普通数组,怎么扩容的?
就是重新申请一个二倍于原数组大小的数组,然后把数据都拷贝过去,并释放原数组内存。(对,就是这么原始粗暴的方法!)
举一个例子,如图:
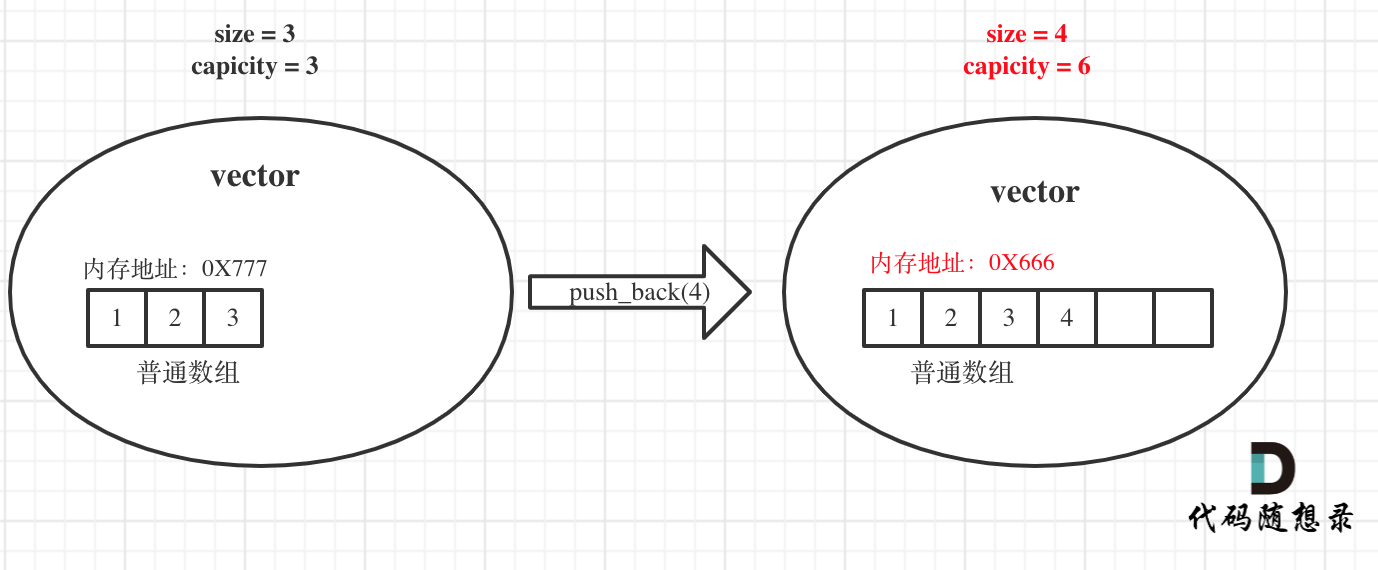
原 vector 中的 size 和 capicity 相同都是 3,初始化为 1 2 3,此时要 push_back 一个元素 4。
那么底层其实就要申请一个大小为 6 的普通数组,并且把原元素拷贝过去,释放原数组内存,注意图中底层数组的内存起始地址已经变了。
同时也注意此时 capicity 和 size 的变化,关键的地方我都标红了。
而在贪心算法:根据身高重建队列 (opens in a new tab)中,我们使用 vector 来做 insert 的操作,此时大家可会发现,虽然表面上复杂度是 O(n^2),但是其底层都不知道额外做了多少次全量拷贝了,所以算上 vector 的底层拷贝,整体时间复杂度可以认为是 O(n^2 + t × n)级别的,t 是底层拷贝的次数。
那么是不是可以直接确定好 vector 的大小,不让它在动态扩容了,例如在贪心算法:根据身高重建队列 (opens in a new tab)中已经给出了有 people.size 这么多的人,可以定义好一个固定大小的 vector,这样我们就可以控制 vector,不让它底层动态扩容。
这种方法需要自己模拟插入的操作,不仅没有直接调用 insert 接口那么方便,需要手动模拟插入操作,而且效率也不高!
手动模拟的过程其实不是很简单的,需要很多细节,我粗略写了一个版本,如下:
// 版本三
// 使用vector,但不让它动态扩容
class Solution {
public:
static bool cmp(const vector<int> a, const vector<int> b) {
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort (people.begin(), people.end(), cmp);
vector<vector<int>> que(people.size(), vector<int>(2, -1));
for (int i = 0; i < people.size(); i++) {
int position = people[i][1];
if (position == que.size() - 1) que[position] = people[i];
else { // 将插入位置后面的元素整体向后移
for (int j = que.size() - 2; j >= position; j--) que[j + 1] = que[j];
que[position] = people[i];
}
}
return que;
}
};耗时如下:

这份代码就是不让 vector 动态扩容,全程我们自己模拟 insert 的操作,大家也可以直观的看出是一个 O(n^2)的方法了。
但这份代码在 leetcode 上统计的耗时甚至比版本一的还高,我们都不让它动态扩容了,为什么耗时更高了呢?
一方面是 leetcode 的耗时统计本来就不太准,忽高忽低的,只能测个大概。
另一方面:可能是就算避免的 vector 的底层扩容,但这个固定大小的数组,每次向后移动元素赋值的次数比方法一中移动赋值的次数要多很多。
因为方法一中一开始数组是很小的,插入操作,向后移动元素次数比较少,即使有偶尔的扩容操作。而方法三每次都是按照最大数组规模向后移动元素的。
所以对于两种使用数组的方法一和方法三,也不好确定谁优,但一定都没有使用方法二链表的效率高!
一波分析之后,对于贪心算法:根据身高重建队列 (opens in a new tab) ,大家就安心使用链表吧!别折腾了,相当于我替大家折腾了一下。
总结
大家应该发现了,编程语言中一个普通容器的 insert,delete 的使用,都可能对写出来的算法的有很大影响!
如果抛开语言谈算法,除非从来不用代码写算法纯分析,否则的话,语言功底不到位 O(n)的算法可以写出 O(n^2)的性能。
相信在这里学习算法的录友们,都是想在软件行业长远发展的,都是要从事编程的工作,那么一定要深耕好一门编程语言,这个非常重要!
其他语言版本
Rust
// 版本二,使用list(链表)
use std::collections::LinkedList;
impl Solution{
pub fn reconstruct_queue(mut people: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
let mut queue = LinkedList::new();
people.sort_by(|a, b| {
if a[0] == b[0] {
return a[1].cmp(&b[1]);
}
b[0].cmp(&a[0])
});
queue.push_back(people[0].clone());
for v in people.iter().skip(1) {
if queue.len() > v[1] as usize {
let mut back_link = queue.split_off(v[1] as usize);
queue.push_back(v.clone());
queue.append(&mut back_link);
} else {
queue.push_back(v.clone());
}
}
queue.into_iter().collect()
}
}Go
Go 中 slice 的append操作和 C++中 vector 的扩容机制基本相同。
说是基本呢,其实是因为大家平时刷题和工作中遇到的数据不会特别大。
具体来说,当当前 slice 的长度小于1024时,执行append操作,新 slice 的 capacity 会变成当前的 2 倍;而当 slice 长度大于等于1024时,slice 的扩容变成了每次增加当前 slice 长度的1/4。
在 Go Slice 的底层实现中,如果 capacity 不够时,会做一个 reslice 的操作,底层数组也会重新被复制到另一块内存区域中,所以append一个元素,不一定是 O(1), 也可能是 O(n)哦。