以为只用了递归，其实还用了回溯

257. 二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例: 257.二叉树的所有路径1

算法公开课

《代码随想录》算法视频公开课 (opens in a new tab)：：递归中带着回溯，你感受到了没？| LeetCode：257. 二叉树的所有路径 (opens in a new tab)，相信结合视频在看本篇题解，更有助于大家对本题的理解。

思路

这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

前序遍历以及回溯的过程如图：

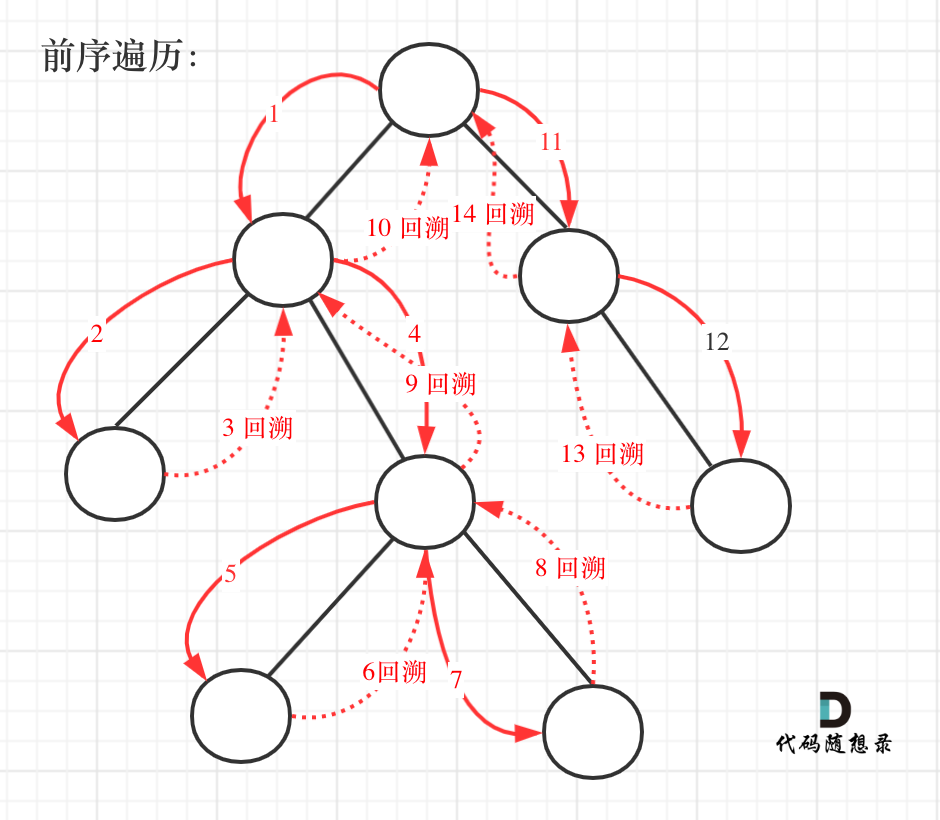
257.二叉树的所有路径

我们先使用递归的方式，来做前序遍历。要知道递归和回溯就是一家的，本题也需要回溯。

递归

递归函数参数以及返回值

要传入根节点，记录每一条路径的 path，和存放结果集的 result，这里递归不需要返回值，代码如下：

void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)

确定递归终止条件

在写递归的时候都习惯了这么写：

if (cur == NULL) {
    终止处理逻辑
}

但是本题的终止条件这样写会很麻烦，因为本题要找到叶子节点，就开始结束的处理逻辑了（把路径放进 result 里）。

那么什么时候算是找到了叶子节点？ 是当 cur 不为空，其左右孩子都为空的时候，就找到叶子节点。

所以本题的终止条件是：

if (cur->left == NULL && cur->right == NULL) {
    终止处理逻辑
}

为什么没有判断 cur 是否为空呢，因为下面的逻辑可以控制空节点不入循环。

再来看一下终止处理的逻辑。

这里使用 vector 结构 path 来记录路径，所以要把 vector 结构的 path 转为 string 格式，再把这个 string 放进 result 里。

那么为什么使用了 vector 结构来记录路径呢？ 因为在下面处理单层递归逻辑的时候，要做回溯，使用 vector 方便来做回溯。

可能有的同学问了，我看有些人的代码也没有回溯啊。

其实是有回溯的，只不过隐藏在函数调用时的参数赋值里，下文我还会提到。

这里我们先使用 vector结构的 path 容器来记录路径，那么终止处理逻辑如下：

if (cur->left == NULL && cur->right == NULL) { // 遇到叶子节点
    string sPath;
    for (int i = 0; i < path.size() - 1; i++) { // 将path里记录的路径转为string格式
        sPath += to_string(path[i]);
        sPath += "->";
    }
    sPath += to_string(path[path.size() - 1]); // 记录最后一个节点（叶子节点）
    result.push_back(sPath); // 收集一个路径
    return;
}

确定单层递归逻辑

因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进 path 中。

path.push_back(cur->val);

然后是递归和回溯的过程，上面说过没有判断 cur 是否为空，那么在这里递归的时候，如果为空就不进行下一层递归了。

所以递归前要加上判断语句，下面要递归的节点是否为空，如下

if (cur->left) {
    traversal(cur->left, path, result);
}
if (cur->right) {
    traversal(cur->right, path, result);
}

此时还没完，递归完，要做回溯啊，因为 path 不能一直加入节点，它还要删节点，然后才能加入新的节点。

那么回溯要怎么回溯呢，一些同学会这么写，如下：

if (cur->left) {
    traversal(cur->left, path, result);
}
if (cur->right) {
    traversal(cur->right, path, result);
}
path.pop_back();

这个回溯就有很大的问题，我们知道，回溯和递归是一一对应的，有一个递归，就要有一个回溯，这么写的话相当于把递归和回溯拆开了，一个在花括号里，一个在花括号外。

所以回溯要和递归永远在一起，世界上最遥远的距离是你在花括号里，而我在花括号外！

那么代码应该这么写：

if (cur->left) {
    traversal(cur->left, path, result);
    path.pop_back(); // 回溯
}
if (cur->right) {
    traversal(cur->right, path, result);
    path.pop_back(); // 回溯
}

那么本题整体代码如下：

// 版本一
class Solution {
private:
 
    void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
        path.push_back(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中
        // 这才到了叶子节点
        if (cur->left == NULL && cur->right == NULL) {
            string sPath;
            for (int i = 0; i < path.size() - 1; i++) {
                sPath += to_string(path[i]);
                sPath += "->";
            }
            sPath += to_string(path[path.size() - 1]);
            result.push_back(sPath);
            return;
        }
        if (cur->left) { // 左
            traversal(cur->left, path, result);
            path.pop_back(); // 回溯
        }
        if (cur->right) { // 右
            traversal(cur->right, path, result);
            path.pop_back(); // 回溯
        }
    }
 
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        vector<int> path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;
    }
};

如上的 C++代码充分体现了回溯。

那么如上代码可以精简成如下代码：

class Solution {
private:
 
    void traversal(TreeNode* cur, string path, vector<string>& result) {
        path += to_string(cur->val); // 中
        if (cur->left == NULL && cur->right == NULL) {
            result.push_back(path);
            return;
        }
        if (cur->left) traversal(cur->left, path + "->", result); // 左
        if (cur->right) traversal(cur->right, path + "->", result); // 右
    }
 
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        string path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;
 
    }
};

如上代码精简了不少，也隐藏了不少东西。

注意在函数定义的时候void traversal(TreeNode* cur, string path, vector<string>& result) ，定义的是string path，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。（这里涉及到 C++语法知识）

那么在如上代码中，貌似没有看到回溯的逻辑，其实不然，回溯就隐藏在traversal(cur->left, path + "->", result);中的 path + "->"。 每次函数调用完，path 依然是没有加上"->" 的，这就是回溯了。

为了把这份精简代码的回溯过程展现出来，大家可以试一试把：

if (cur->left) traversal(cur->left, path + "->", result); // 左  回溯就隐藏在这里

改成如下代码：

path += "->";
traversal(cur->left, path, result); // 左

即：

if (cur->left) {
    path += "->";
    traversal(cur->left, path, result); // 左
}
if (cur->right) {
    path += "->";
    traversal(cur->right, path, result); // 右
}

此时就没有回溯了，这个代码就是通过不了的了。

如果想把回溯加上，就要在上面代码的基础上，加上回溯，就可以 AC 了。

if (cur->left) {
    path += "->";
    traversal(cur->left, path, result); // 左
    path.pop_back(); // 回溯 '>'
    path.pop_back(); // 回溯 '-'
}
if (cur->right) {
    path += "->";
    traversal(cur->right, path, result); // 右
    path.pop_back(); // 回溯 '>'
    path.pop_back(); //  回溯 '-'
}

整体代码如下：

//版本二
class Solution {
private:
    void traversal(TreeNode* cur, string path, vector<string>& result) {
        path += to_string(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中
        if (cur->left == NULL && cur->right == NULL) {
            result.push_back(path);
            return;
        }
        if (cur->left) {
            path += "->";
            traversal(cur->left, path, result); // 左
            path.pop_back(); // 回溯 '>'
            path.pop_back(); // 回溯 '-'
        }
        if (cur->right) {
            path += "->";
            traversal(cur->right, path, result); // 右
            path.pop_back(); // 回溯'>'
            path.pop_back(); // 回溯 '-'
        }
    }
 
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        string path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;
 
    }
};

大家应该可以感受出来，如果把 path + "->"作为函数参数就是可以的，因为并没有改变 path 的数值，执行完递归函数之后，path 依然是之前的数值（相当于回溯了）

综合以上，第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里，第一种递归写法虽然代码多一些，但是把每一个逻辑处理都完整的展现出来了。

拓展

这里讲解本题解的写法逻辑以及一些更具体的细节，下面的讲解中，涉及到 C++语法特性，如果不是 C++的录友，就可以不看了，避免越看越晕。

如果是 C++的录友，建议本题独立刷过两遍，再看下面的讲解，同样避免越看越晕，造成不必要的负担。

在第二版本的代码中，其实仅仅是回溯了 -> 部分（调用两次 pop_back，一个 pop> 一次 pop-），大家应该疑惑那么 path += to_string(cur->val); 这一步为什么没有回溯呢？一条路径能持续加节点不做回溯吗？

其实关键还在于参数，使用的是 string path，这里并没有加上引用& ，即本层递归中，path + 该节点数值，但该层递归结束，上一层 path 的数值并不会受到任何影响。如图所示：

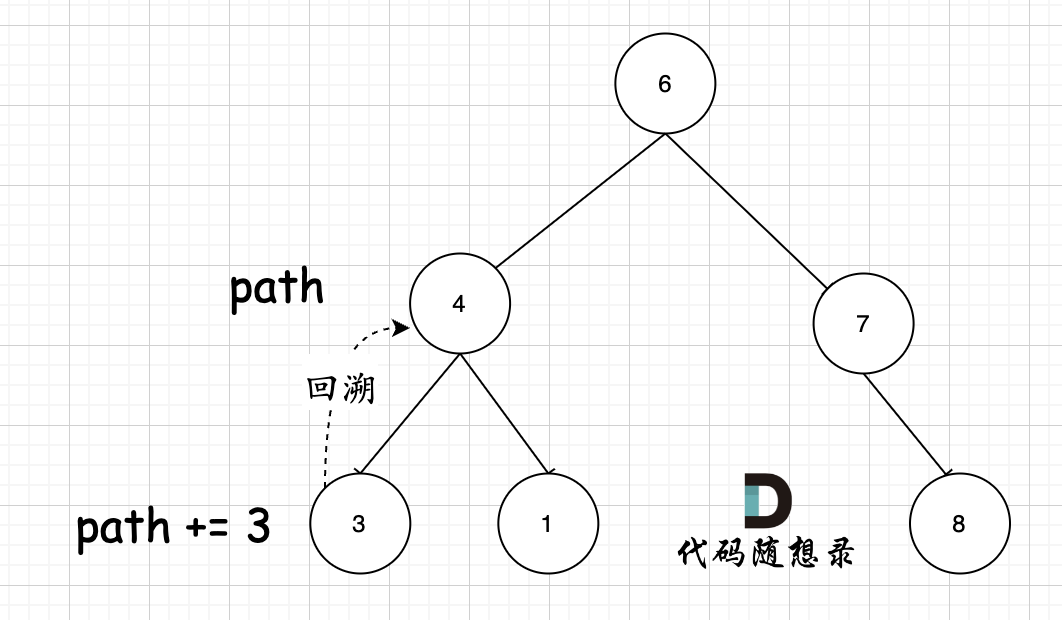
节点 4 的 path，在遍历到节点 3，path+3，遍历节点 3 的递归结束之后，返回节点 4（回溯的过程），path 并不会把 3 加上。

所以这是参数中，不带引用，不做地址拷贝，只做内容拷贝的效果。（这里涉及到 C++引用方面的知识）

在第一个版本中，函数参数我就使用了引用，即 vector<int>& path ，这是会拷贝地址的，所以本层递归逻辑如果有path.push_back(cur->val); 就一定要有对应的 path.pop_back()

那有同学可能想，为什么不去定义一个 string& path 这样的函数参数呢，然后也可能在递归函数中展现回溯的过程，但关键在于，path += to_string(cur->val); 每次是加上一个数字，这个数字如果是个位数，那好说，就调用一次path.pop_back()，但如果是十位数，百位数，千位数呢？百位数就要调用三次path.pop_back()，才能实现对应的回溯操作，这样代码实现就太冗余了。

所以，第一个代码版本中，我才使用 vector 类型的 path，这样方便给大家演示代码中回溯的操作。 vector 类型的 path，不管每次路径收集的数字是几位数，总之一定是 int，所以就一次 pop_back 就可以。

迭代法

至于非递归的方式，我们可以依然可以使用前序遍历的迭代方式来模拟遍历路径的过程，对该迭代方式不了解的同学，可以看文章二叉树：听说递归能做的，栈也能做！ (opens in a new tab)和二叉树：前中后序迭代方式统一写法 (opens in a new tab)。

这里除了模拟递归需要一个栈，同时还需要一个栈来存放对应的遍历路径。

C++代码如下：

class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        stack<TreeNode*> treeSt;// 保存树的遍历节点
        stack<string> pathSt;   // 保存遍历路径的节点
        vector<string> result;  // 保存最终路径集合
        if (root == NULL) return result;
        treeSt.push(root);
        pathSt.push(to_string(root->val));
        while (!treeSt.empty()) {
            TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
            string path = pathSt.top();pathSt.pop();    // 取出该节点对应的路径
            if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
                result.push_back(path);
            }
            if (node->right) { // 右
                treeSt.push(node->right);
                pathSt.push(path + "->" + to_string(node->right->val));
            }
            if (node->left) { // 左
                treeSt.push(node->left);
                pathSt.push(path + "->" + to_string(node->left->val));
            }
        }
        return result;
    }
};

当然，使用 java 的同学，可以直接定义一个成员变量为 object 的栈Stack<Object> stack = new Stack<>();，这样就不用定义两个栈了，都放到一个栈里就可以了。

总结

本文我们开始初步涉及到了回溯，很多同学过了这道题目，可能都不知道自己其实使用了回溯，回溯和递归都是相伴相生的。

我在第一版递归代码中，把递归与回溯的细节都充分的展现了出来，大家可以自己感受一下。

第二版递归代码对于初学者其实非常不友好，代码看上去简单，但是隐藏细节于无形。

最后我依然给出了迭代法。

对于本题充分了解递归与回溯的过程之后，有精力的同学可以再去实现迭代法。

其他语言版本

Java：

//解法一
 
//方式一
class Solution {
    /**
     * 递归法
     */
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();// 存最终的结果
        if (root == null) {
            return res;
        }
        List<Integer> paths = new ArrayList<>();// 作为结果中的路径
        traversal(root, paths, res);
        return res;
    }
 
    private void traversal(TreeNode root, List<Integer> paths, List<String> res) {
        paths.add(root.val);// 前序遍历，中
        // 遇到叶子结点
        if (root.left == null && root.right == null) {
            // 输出
            StringBuilder sb = new StringBuilder();// StringBuilder用来拼接字符串，速度更快
            for (int i = 0; i < paths.size() - 1; i++) {
                sb.append(paths.get(i)).append("->");
            }
            sb.append(paths.get(paths.size() - 1));// 记录最后一个节点
            res.add(sb.toString());// 收集一个路径
            return;
        }
        // 递归和回溯是同时进行，所以要放在同一个花括号里
        if (root.left != null) { // 左
            traversal(root.left, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
        if (root.right != null) { // 右
            traversal(root.right, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
    }
}
 
//方式二
class Solution {
 
    List<String> result = new ArrayList<>();
 
    public List<String> binaryTreePaths(TreeNode root) {
        deal(root, "");
        return result;
    }
 
    public void deal(TreeNode node, String s) {
        if (node == null)
            return;
        if (node.left == null && node.right == null) {
            result.add(new StringBuilder(s).append(node.val).toString());
            return;
        }
        String tmp = new StringBuilder(s).append(node.val).append("->").toString();
        deal(node.left, tmp);
        deal(node.right, tmp);
    }
}

// 解法二
class Solution {
    /**
     * 迭代法
     */
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> result = new ArrayList<>();
        if (root == null)
            return result;
        Stack<Object> stack = new Stack<>();
        // 节点和路径同时入栈
        stack.push(root);
        stack.push(root.val + "");
        while (!stack.isEmpty()) {
            // 节点和路径同时出栈
            String path = (String) stack.pop();
            TreeNode node = (TreeNode) stack.pop();
            // 若找到叶子节点
            if (node.left == null && node.right == null) {
                result.add(path);
            }
            //右子节点不为空
            if (node.right != null) {
                stack.push(node.right);
                stack.push(path + "->" + node.right.val);
            }
            //左子节点不为空
            if (node.left != null) {
                stack.push(node.left);
                stack.push(path + "->" + node.left.val);
            }
        }
        return result;
    }
}

Python:

递归法+回溯

# Definition for a binary tree node.
class Solution:
    def traversal(self, cur, path, result):
        path.append(cur.val)  # 中
        if not cur.left and not cur.right:  # 到达叶子节点
            sPath = '->'.join(map(str, path))
            result.append(sPath)
            return
        if cur.left:  # 左
            self.traversal(cur.left, path, result)
            path.pop()  # 回溯
        if cur.right:  # 右
            self.traversal(cur.right, path, result)
            path.pop()  # 回溯

    def binaryTreePaths(self, root):
        result = []
        path = []
        if not root:
            return result
        self.traversal(root, path, result)
        return result

递归法+隐形回溯（版本一）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
from typing import List, Optional

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        if not root:
            return []
        result = []
        self.traversal(root, [], result)
        return result

    def traversal(self, cur: TreeNode, path: List[int], result: List[str]) -> None:
        if not cur:
            return
        path.append(cur.val)
        if not cur.left and not cur.right:
            result.append('->'.join(map(str, path)))
        if cur.left:
            self.traversal(cur.left, path[:], result)
        if cur.right:
            self.traversal(cur.right, path[:], result)

递归法+隐形回溯（版本二）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def binaryTreePaths(self, root: TreeNode) -> List[str]:
        path = ''
        result = []
        if not root: return result
        self.traversal(root, path, result)
        return result

    def traversal(self, cur: TreeNode, path: str, result: List[str]) -> None:
        path += str(cur.val)
        # 若当前节点为leave，直接输出
        if not cur.left and not cur.right:
            result.append(path)

        if cur.left:
            # + '->' 是隐藏回溯
            self.traversal(cur.left, path + '->', result)

        if cur.right:
            self.traversal(cur.right, path + '->', result)

迭代法：

class Solution:

    def binaryTreePaths(self, root: TreeNode) -> List[str]:
        # 题目中节点数至少为1
        stack, path_st, result = [root], [str(root.val)], []

        while stack:
            cur = stack.pop()
            path = path_st.pop()
            # 如果当前节点为叶子节点，添加路径到结果中
            if not (cur.left or cur.right):
                result.append(path)
            if cur.right:
                stack.append(cur.right)
                path_st.append(path + '->' + str(cur.right.val))
            if cur.left:
                stack.append(cur.left)
                path_st.append(path + '->' + str(cur.left.val))

        return result

Go：

递归法：

func binaryTreePaths(root *TreeNode) []string {
    res := make([]string, 0)
    var travel func(node *TreeNode, s string)
    travel = func(node *TreeNode, s string) {
        if node.Left == nil && node.Right == nil {
            v := s + strconv.Itoa(node.Val)
            res = append(res, v)
            return
        }
        s = s + strconv.Itoa(node.Val) + "->"
        if node.Left != nil {
            travel(node.Left, s)
        }
        if node.Right != nil {
            travel(node.Right, s)
        }
    }
    travel(root, "")
    return res
}

迭代法：

func binaryTreePaths(root *TreeNode) []string {
	stack := []*TreeNode{}
	paths := make([]string, 0)
	res := make([]string, 0)
	if root != nil {
		stack = append(stack, root)
		paths = append(paths, "")
	}
	for len(stack) > 0 {
		l := len(stack)
		node := stack[l-1]
		path := paths[l-1]
		stack = stack[:l-1]
		paths = paths[:l-1]
		if node.Left == nil && node.Right == nil {
			res = append(res, path+strconv.Itoa(node.Val))
			continue
		}
		if node.Right != nil {
			stack = append(stack, node.Right)
			paths = append(paths, path+strconv.Itoa(node.Val)+"->")
		}
		if node.Left != nil {
			stack = append(stack, node.Left)
			paths = append(paths, path+strconv.Itoa(node.Val)+"->")
		}
	}
	return res
}

JavaScript:

递归法：

var binaryTreePaths = function (root) {
  //递归遍历+递归三部曲
  let res = [];
  //1. 确定递归函数 函数参数
  const getPath = function (node, curPath) {
    //2. 确定终止条件，到叶子节点就终止
    if (node.left === null && node.right === null) {
      curPath += node.val;
      res.push(curPath);
      return;
    }
    //3. 确定单层递归逻辑
    curPath += node.val + "->";
    node.left && getPath(node.left, curPath);
    node.right && getPath(node.right, curPath);
  };
  getPath(root, "");
  return res;
};

迭代法：

var binaryTreePaths = function (root) {
  if (!root) return [];
  const stack = [root],
    paths = [""],
    res = [];
  while (stack.length) {
    const node = stack.pop();
    let path = paths.pop();
    if (!node.left && !node.right) {
      // 到叶子节点终止, 添加路径到结果中
      res.push(path + node.val);
      continue;
    }
    path += node.val + "->";
    if (node.right) {
      // 右节点存在
      stack.push(node.right);
      paths.push(path);
    }
    if (node.left) {
      // 左节点存在
      stack.push(node.left);
      paths.push(path);
    }
  }
  return res;
};

TypeScript：

递归法

function binaryTreePaths(root: TreeNode | null): string[] {
  function recur(node: TreeNode, route: string, resArr: string[]): void {
    route += String(node.val);
    if (node.left === null && node.right === null) {
      resArr.push(route);
      return;
    }
    if (node.left !== null) recur(node.left, route + "->", resArr);
    if (node.right !== null) recur(node.right, route + "->", resArr);
  }
  const resArr: string[] = [];
  if (root === null) return resArr;
  recur(root, "", resArr);
  return resArr;
}

迭代法

// 迭代法2
function binaryTreePaths(root: TreeNode | null): string[] {
  let helperStack: TreeNode[] = [];
  let tempNode: TreeNode;
  let routeArr: string[] = [];
  let resArr: string[] = [];
  if (root !== null) {
    helperStack.push(root);
    routeArr.push(String(root.val));
  }
  while (helperStack.length > 0) {
    tempNode = helperStack.pop()!;
    let route: string = routeArr.pop()!; // tempNode 对应的路径
    if (tempNode.left === null && tempNode.right === null) {
      resArr.push(route);
    }
    if (tempNode.right !== null) {
      helperStack.push(tempNode.right);
      routeArr.push(route + "->" + tempNode.right.val); // tempNode.right 对应的路径
    }
    if (tempNode.left !== null) {
      helperStack.push(tempNode.left);
      routeArr.push(route + "->" + tempNode.left.val); // tempNode.left 对应的路径
    }
  }
  return resArr;
}

Swift:

递归/回溯

func binaryTreePaths(_ root: TreeNode?) -> [String] {
    var res = [String]()
    guard let root = root else {
        return res
    }
    var path = [Int]()
    _binaryTreePaths(root, path: &path, res: &res)
    return res
}
func _binaryTreePaths(_ root: TreeNode, path: inout [Int], res: inout [String]) {
    path.append(root.val)
    if root.left ==  nil && root.right == nil {
        var str = ""
        for i in 0 ..< path.count - 1 {
            str.append("\(path[i])->")
        }
        str.append("\(path.last!)")
        res.append(str)
        return
    }
    if let left = root.left {
        _binaryTreePaths(left, path: &path, res: &res)
        path.removeLast()
    }
    if let right = root.right {
        _binaryTreePaths(right, path: &path, res: &res)
        path.removeLast()
    }
}

迭代

func binaryTreePaths(_ root: TreeNode?) -> [String] {
    var res = [String]()
    guard let root = root else {
        return res
    }
    var stackNode = [TreeNode]()
    stackNode.append(root)
 
    var stackStr = [String]()
    stackStr.append("\(root.val)")
 
    while !stackNode.isEmpty {
        let node = stackNode.popLast()!
        let str = stackStr.popLast()!
        if node.left == nil && node.right == nil {
            res.append(str)
        }
        if let left = node.left {
            stackNode.append(left)
            stackStr.append("\(str)->\(left.val)")
        }
        if let right = node.right {
            stackNode.append(right)
            stackStr.append("\(str)->\(right.val)")
        }
    }
    return res
}

Scala:

递归:

object Solution {
  import scala.collection.mutable.ListBuffer
  def binaryTreePaths(root: TreeNode): List[String] = {
    val res = ListBuffer[String]()
    def traversal(curNode: TreeNode, path: ListBuffer[Int]): Unit = {
      path.append(curNode.value)
      if (curNode.left == null && curNode.right == null) {
        res.append(path.mkString("->")) // mkString函数: 将数组的所有值按照指定字符串拼接
        return // 处理完可以直接return
      }
 
      if (curNode.left != null) {
        traversal(curNode.left, path)
        path.remove(path.size - 1)
      }
      if (curNode.right != null) {
        traversal(curNode.right, path)
        path.remove(path.size - 1)
      }
    }
    traversal(root, ListBuffer[Int]())
    res.toList
  }
}

Rust:

// 递归
impl Solution {
    pub fn binary_tree_paths(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<String> {
        let mut res = vec![];
        Self::recur(&root, String::from(""), &mut res);
        res
    }
    pub fn recur(node: &Option<Rc<RefCell<TreeNode>>>, mut path: String, res: &mut Vec<String>) {
        let r = node.as_ref().unwrap().borrow();
        path += format!("{}", r.val).as_str();
        if r.left.is_none() && r.right.is_none() {
            res.push(path.to_string());
            return;
        }
        if r.left.is_some() {
            Self::recur(&r.left, path.clone() + "->", res);
        }
        if r.right.is_some() {
            Self::recur(&r.right, path + "->", res);
        }
    }
}

C#

public IList<string> BinaryTreePaths(TreeNode root)
{
    List<int> path = new();
    List<string> res = new();
    if (root == null) return res;
    Traversal(root, path, res);
    return res;
}
public void Traversal(TreeNode node, List<int> path, List<string> res)
{
    path.Add(node.val);
    if (node.left == null && node.right == null)
    {
        string sPath = "";
        for (int i = 0; i < path.Count - 1; i++)
        {
            sPath += path[i].ToString();
            sPath += "->";
        }
        sPath += path[path.Count - 1].ToString();
        res.Add(sPath);
        return;
    }
    if (node.left != null)
    {
        Traversal(node.left, path, res);
        path.RemoveAt(path.Count-1);
    }
    if (node.right != null)
    {
        Traversal(node.right, path, res);
        path.RemoveAt(path.Count-1);
    }
}

01. 数组理论基础